Part 1에 이어서 구글 머신러닝 crash course를 정리하려고 한다. 그럼 시작~~

과적합(over fitting)의 위험성
데이터를 과적합한다면 오히려 정확도가 떨어지는 모델을 만들게 된다. 과적합에 유의하자!
학습 데이터와 테스트 데이터로 데이터 분할하기

- 학습 데이터는 모델을 학습시키기 위한 데이터이고 테스트 데이터는 학습된 모델을 테스트하는 데이터.
- 테스트 데이터는 두가지 조건을 충족해야한다.
- 충분히 큰 데이터.
- 학습 데이터와 특성이 같은 데이터.
학습데이터와 검증 데이터와 테스트 데이터로 데이터 분할하기 : 과적합 가능성을 줄입니다!

- 학습 데이터는 모델을 학습시키기 위한 데이터, 검증 데이터는 학습된 모델을 검증하는 데이터, 테스트 데이터는 학습 후 검증된 모델을 테스트하는 데이터.
- 순서가 ‘1. 학습 데이터로 모델 학습, 2. 검증 데이터로 학습된 모델 검증, 3. 테스트 데이터로 검증된 모델 확인’로 된다.
Feature Engineering, feature 다듬기, 실데이터 다듬기
더 정확한 모델을 만드는데 기초가 되는 것은 feature을 다듬고 정확한 데이터를 모델에 넣어주는 것이다. 이를 위해 Feature Engineering이 필요하다. Feature Engineering, 말은 거창해보이지만 실데이터를 모델에 넣어줄 수 있도록 숫자나 특정 글자로 데이터를 변환하거나 필요없는 데이터를 버리거나 누락된 데이터 등을 처리하는 작업을 말한다.
Feature Engineering은 시간이 많이 걸리고(보통 75%의 머신러닝 프로젝트의 시간이 여기에 쓰인다고 함) 어떤 데이터가 중요한지, 어떤 데이터에 초점을 맞춰서 학습을 진행할 것인지 결정한 후 해야하는 작업(데이터 다듬기는 당연히 어떤 데이터가 모델 학습에 필요한지 정하고 해야하는 작업이겠죠? ㅎㅎ)이라 머신러닝 전 학습에 쓰일 데이터들을 준비하는 단계에서 진행해야하는 정말 중요한 작업이다.
Feature Engineering 예시
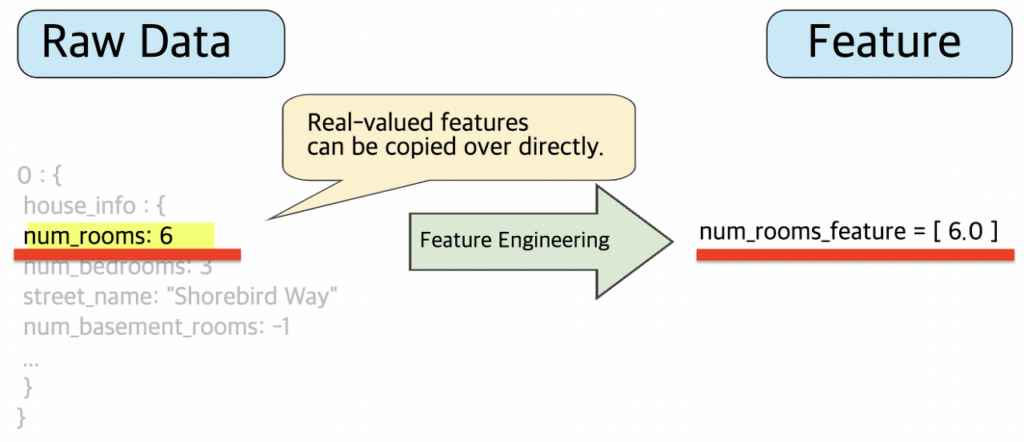
1. 숫자 값 매핑
2. 범주형 값 매핑
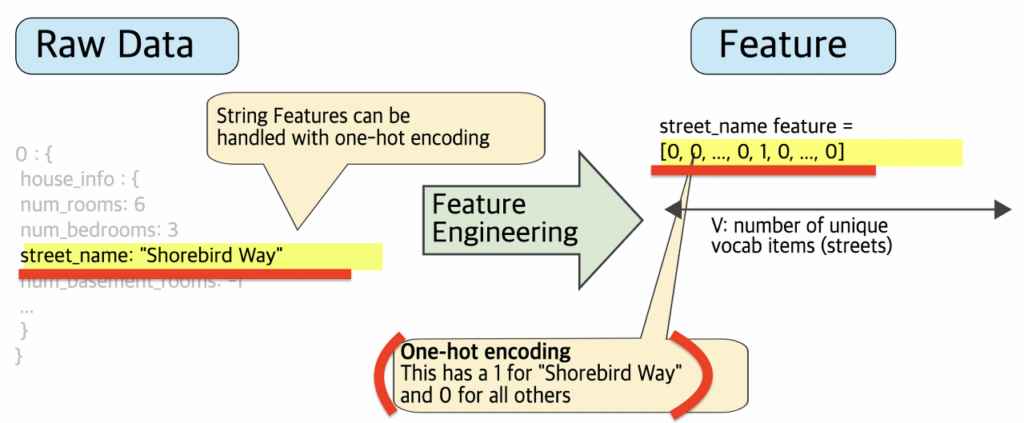
실데이터 street name(거리 이름)이 {‘Charleston Road’, ‘North Shoreline Boulevard’, ‘Shorebird Way’, ‘Rengstorff Avenue’} 카테고리로 나눠질 수 있다면 거리 이름을 원-핫 인코딩(one-hot encoding)을 한다.
- 원-핫 인코딩: 벡터 값이 1인 것이 하나이고 나머지는 0인 것.
- 멀티-핫 인코딩: 벡터 값이 1인 것이 여러 개, 나머지는 0인 것.
- 원-핫 인코딩 예시
- Charleston Road -> [1,0,0,0]
- North Shoreline Boulevard -> [0,1,0,0]
- Shorebird Way -> [0,0,1,0]
- Rengstorff Avenue -> [0,0,0,1]
- 만약 두개의 street 사이에 있는 값을 나타내고 싶으면(Charleston Road, North Shoreline Boulevard 사이) 벡터로는 [1,1,0,0]로 나타낸다.
3. 모델 학습에 중요한 데이터만 남기고 나머지 데이터들은 버린다.

어떤 모델 학습이던 모델 학습에 기기 번호는 중요하지 않다(그냥 랜덤한 번호이기 때문). 모델 학습엔 카테고리로 분류되는 feature들이 쓰인다. 예를 들면 기기의 종류(device model)이 모델 학습에 사용된다.
4. 데이터는 정확하고 분명해야한다.

유저의 나이가 23인 것은 말이 되지만 123456789인 것은 말이 안된다(불가능하다). 이런 것들은 데이터로 쓸 수 없다. 사람은 그렇게 오래 살 수 없다(미래에는 오래 살 수도 있겠지만 지금 평균 연령이 80정도임).
5. 데이터가 존재하는지 안하는지 그것에 대한 Bool 기능을 만들고 그 다음에 feature 값을 만들어라.

데이터가 존재하지 않는다고 -1.0으로 feature 값을 만들면 안된다. 이 경우 Bool 기능(참/거짓, 0/1)을 추가해 Bool이 참일 경우에만 feature 값(watch_time)이 만들어지도록 해야한다(watch_time_is_defined가 1.0인 것은 참이라는 것이고 이 경우에만 watch_time을 feature 값으로 준다).
6. 시간이 지나도 변하지 않는 feature을 설정하자.

city id(도시 이름)을 숫자로 적고 나중에 그것이 바꾸는 것보다 string(문자열)로 적는 것이 현명하다(외국은 시간이 지나면 도시 번호가 바뀌나보다. 예시를 그냥 구글 머신러닝 crash course 기초과정에서 들고와서 우리나라에서 이해가 되지 않는 것들이 있다 ㅎㅎ). feature이 바뀌지 않게 하자.
7. 꼭 필요한 x값(feature 값)만 데이터로 가지도록 한다(x축(feature 축)이 쓸데없이 길지 않도록 조정한다).
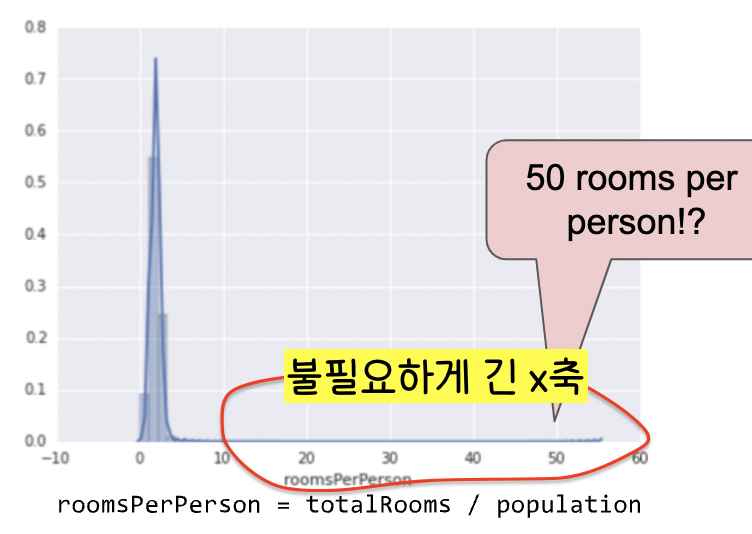
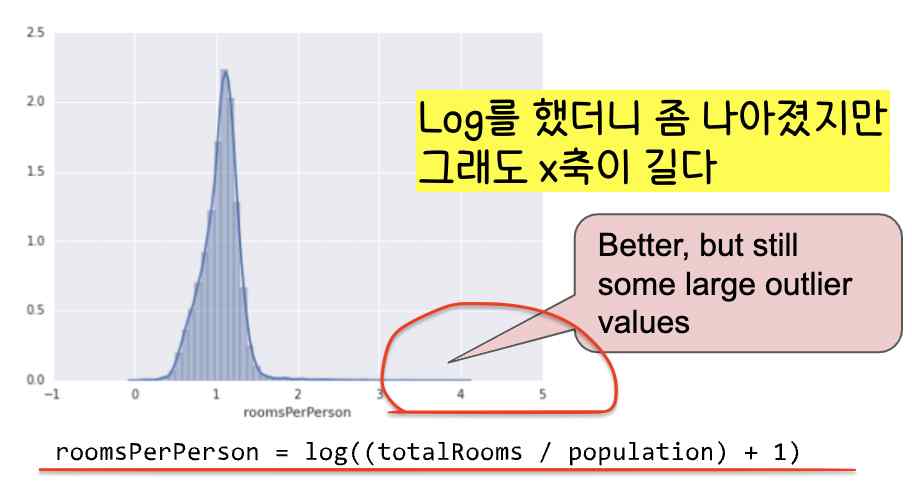

8. Feature과 Label 값이 선형 관계가 아니라면 Binning을 적용한다(범주형 값 매핑과 비슷)
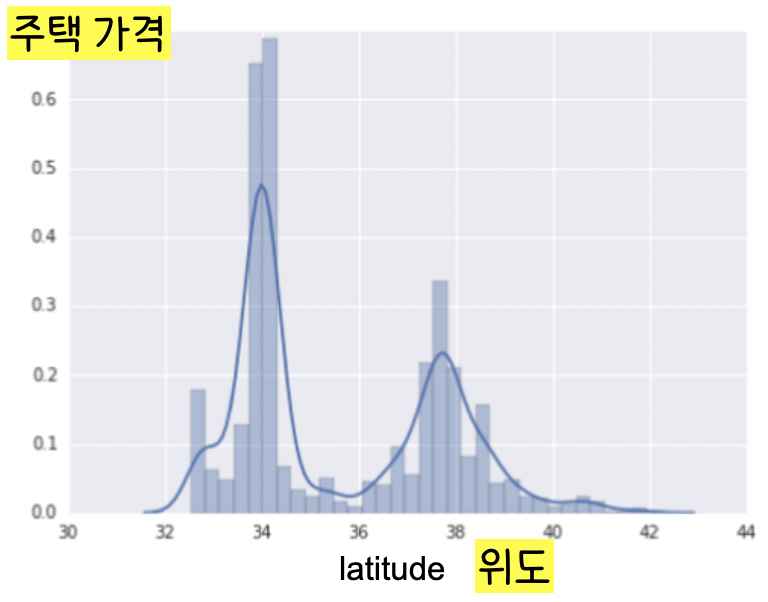
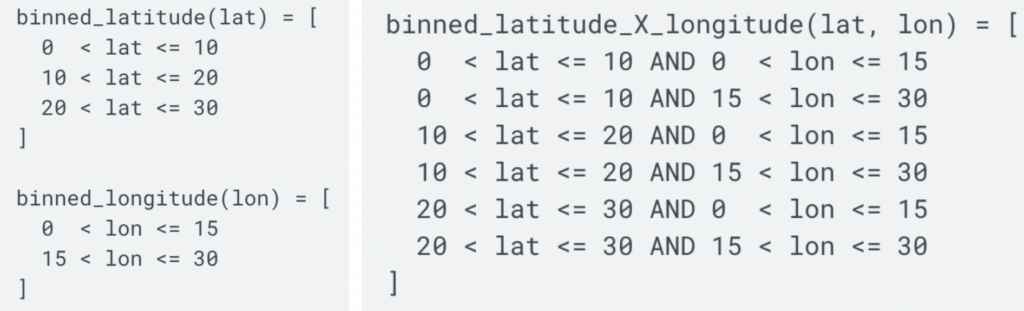
Feature(위도)와 Label(주택 가격)은 선형 관계가 아니다(=위도가 높아진다고 선형적으로 주택 가격이 높아지지 않는다). 이 경우 2번에서 원-핫 인코딩을 했던 {‘Charleston Road’, ‘North Shoreline Boulevard’, ‘Shorebird Way’, ‘Rengstorff Avenue’} 예시와 비슷하게 위도를 카테고리로 나누어 원-핫 인코딩을 하는 것을 Binning이라고 한다.
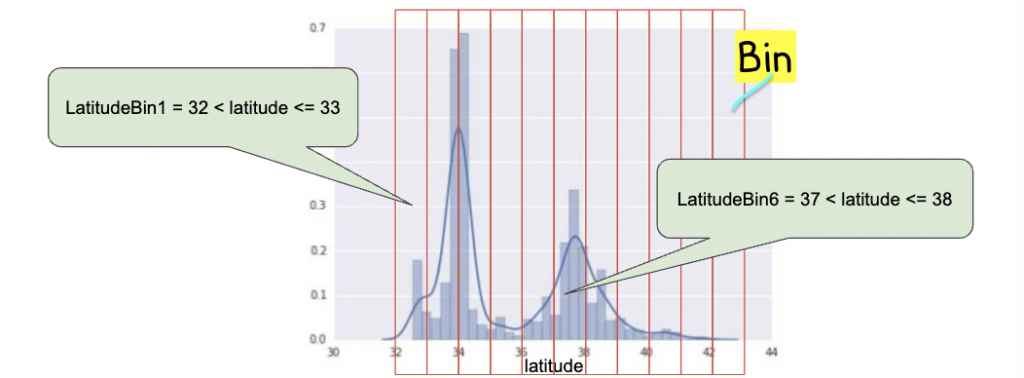
Bin은 x축 그래프의 구간(interval, cell)을 지칭하는 말로 Binning은 데이터 그래프를 여러 개의 카테고리로 나누어 그 카테고리 안에 속하는 feature은 같은 벡터로 나타내도록 하는 것이다(예시: [0,0,0,0,0,1,0,0,0,0,0] 같은 벡터로 만듦). 여기선 11개의 bin으로 나누었다. 위도가 37와 38 사이이면 어느 값이던, 37.1이던 37.5이던 같이 [0,0,0,0,0,1,0,0,0,0,0] 벡터로 표시한다.
9. 스크러빙(누락된 값, 중복 예시, 잘못된 라벨, 잘못된 특성 값) 해결
어떤 데이터가 정확하지 않거나 잘못되었을 경우 데이터에서 그 값을 삭제하여 정확한 데이터 셋을 만든다.
히스토그램은 데이터를 시각화하는데 큰 도움을 주므로
- 데이터의 최대 값, 최소 값
- 데이터의 평균, 중앙값
- 표준 편차
등을 알아내 그 값들이 적절한지 확인해보고 그렇지 않다면 데이터를 재확인해본다.
!!좋은 데이터는 머신 러닝에 필수!!
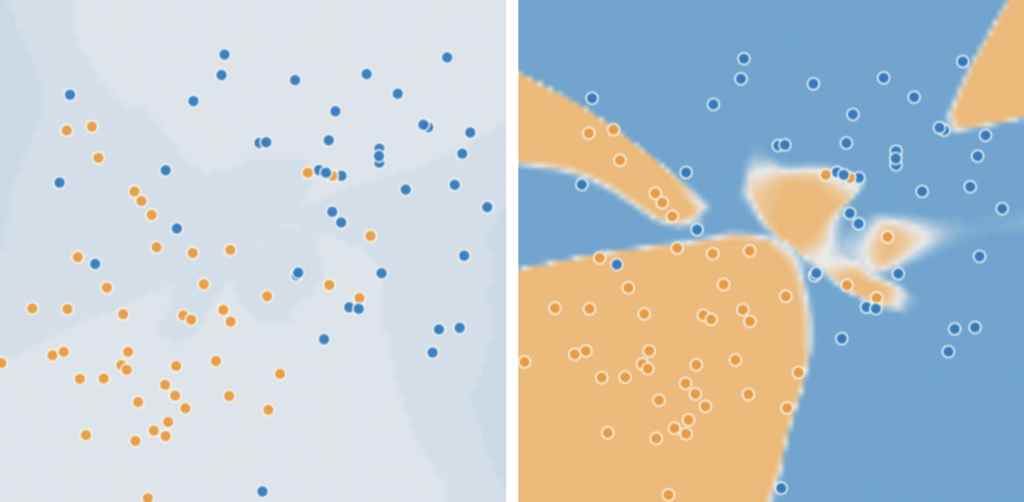
특성 교차: 비선형 문제에 적합
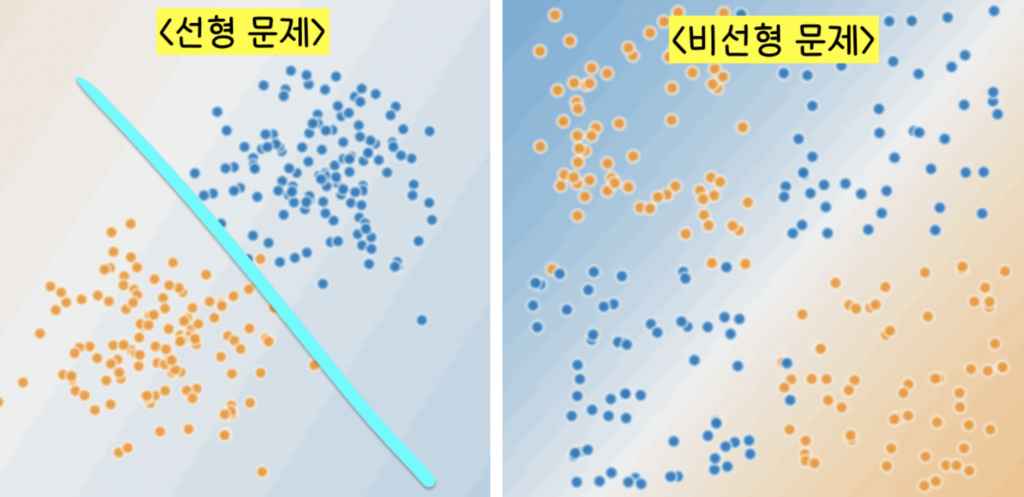
왼쪽 그림의 주황색, 파란색 데이터는 서로 특성이 다르다. 주황색은 스팸이 아닌 메일이고 파란 색은 스팸 메일을 나타낸다. 왼쪽 그림은 이 두 데이터를 하나의 선(형광 파란색)으로 특징별로 나눌 수 있지만 오른쪽 그림은 특징이 다른 데이터셋을 하나의 선으로 특징별로 나눌 수 없다. 이런 비선형 문제는 어떻게 풀어야할까?
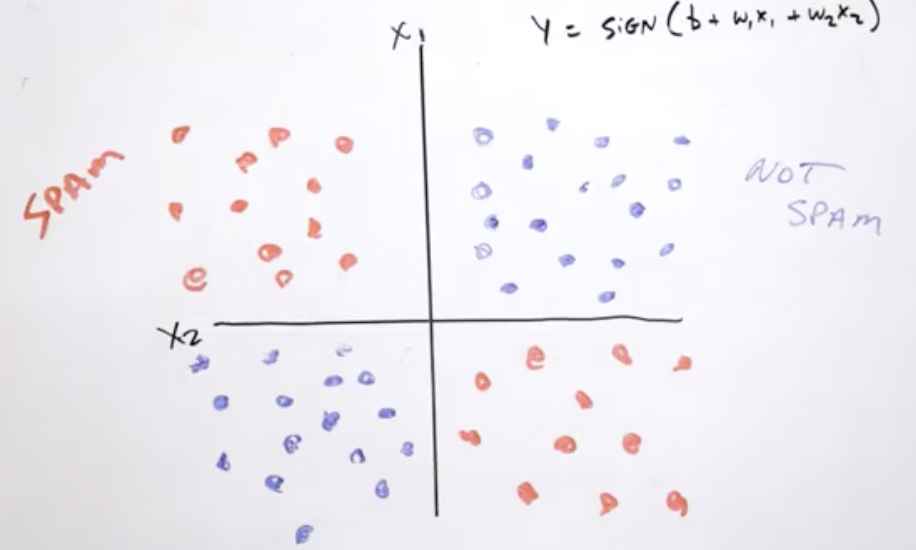
이런 비선형 문제의 경우 합성 feature(x3)을 만드는 것이 답이다. x3 = x1*x2로 이 합성 feature은 특성 교차(feature cross)라고 부른다. 이 특성 교차를 이용해 label(y값)을 구하면 y = b + w1x1 + w2x2 + w3x3로 나타낼 수 있다.
특성교차는
- [A x B] : 두 특성(feature)을 곱해서 만든 특성 교차
- [A x B x C x D x E] : 다섯 개의 특성을 곱해서 만든 특성 교차
- [A x A] : 하나의 특성을 두 번 곱해서 만든 특성 교차
등으로 나타낼 수 있다. 이렇게만 말하면 특성 교차를 뭐하러 쓰나 도대체 이해가 안 갈 수 있으니 예시를 들어보자면
우리가 만약 동물 주인의 만족도(y값, label)를 측정하는 머신러닝 모델을 만든다고 치고 특성(x값, feature)들을 동물의 행동 유형(x1)과 시간(x2)이라고 정한다면 이 모델을 학습시키는데 동물의 행동 유형 또는 시간을 따로 따로 feature 값으로 주어서 동물 주인의 만족도를 측정하는 것보다 시간에 따른 동물의 행동 유형(x1*x2)로 특성 교차를 이용해 동물 주인의 만족도를 측정하는 것이 더 정확하고 합리적인 머신러닝 모델을 만들 수 있다는 것이다.
내가 퇴근해서 집에 왔을 때 내가 키우는 동물이 나를 보고 행복해서 반기며 우는 것과 새벽 3시에 내가 자고있는데 외부 소리에 반응해서 옆집 사람을 깨울만큼 짖는 것이 내가 키우는 동물에 대한 만족도를 측정하는데 크게 기여한다는 뜻이다. 이 경우 [동물의 행동 유형 x 시간]을 특성 교차로 머신러닝에 쓰는 것이 바람직하다.
특성교차의 연산은 아래와 같이 한다.
L2 정규화: 과적합 방지하기!
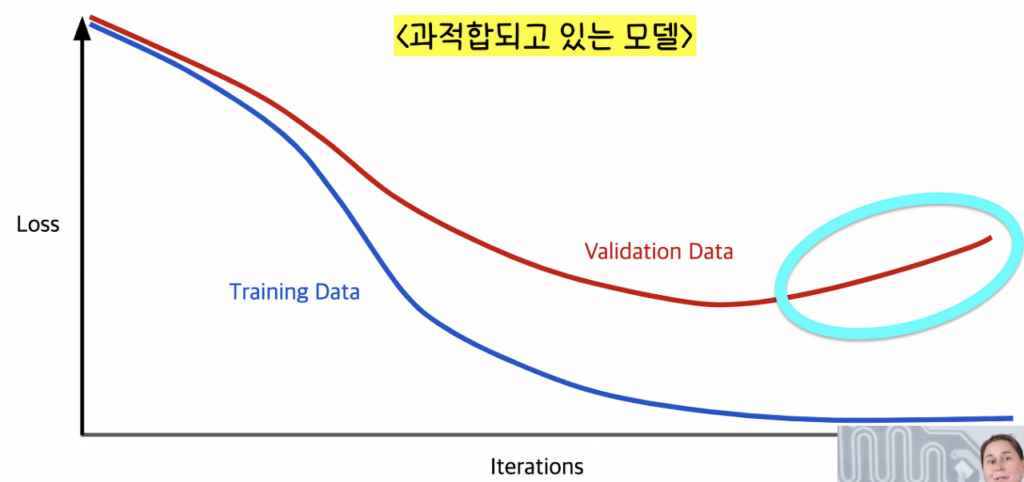
모델이 과적합되었다는 의미를 해석하자면 우리가 영어를 영어가 모국어인 한 명의 10대 청소년에게 계속 배우는 것과 비슷하다고 말할 수 있다. 처음에는 이 한 명의 10대 청소년이 나의 영어 실력에 엄청난 도움이 될테지만 계속 이 한 명의 10대 청소년에게 영어를 배운다면 이 청소년의 악센트, 슬랭(비속어)까지 배우게되어 궁극적인 나의 영어실력에는 도움이 되지 않을 수 있다. 모델이 Generalize된 것만 배우는 것이 아닌 지극히 개인적이고 특징적인 것까지 배우게되는 것을 모델이 과적합(Overfitting)되었다고 말할 수 있다.
그렇다면 이 과적합을 어떻게 하면 막을 수 있을까? 과적합을 막기 위해선 정규화(regularization)를 하는 것이 답이다.
정규화는
- 과적합이 이루어지기 전에 모델이 학습을 멈추게 하는 방법과
- 학습을 계속하면서 모델의 복잡도에 패널티를 주는 방법이 있다.
정규화 방법 중 오늘은 L2 정규화에 대해 알아보겠다. L2 정규화는 모델의 복잡도를 가중치(weight) 제곱의 합으로 나타낸다. 가중치들의 값이 w1 = 0.2, w2 = 0.5, w3 = 5, w4 = 1, w5 = 0.25, w6 = 0.75이라면 L2 정규화 항은 아래와 같이 나타낼 수 있다.

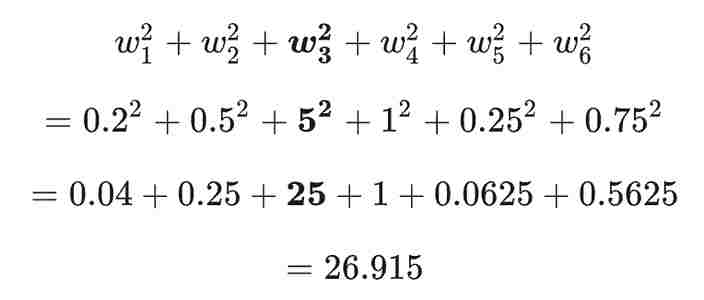
위의 수식에서 볼 수 있듯이 w1,w2,w5,w6는 가중치가 0에 가까워서 모델의 복잡도에 거의 영향을 주지 않지만 w3의 경우 모델의 복잡도에 큰 영향을 미칠 수 있다(w3의 제곱 값이 25이다).
지금까지 우리는 모델의 Loss 값만 최소로 줄이기 위해 노력했지만 이제는 모델의 과적합도 방지하기 위해 L2 정규화도 신경써야한다. 따라서 우리가 최소 값으로 나타내고자 하는 값은 Loss 값 + L2 정규화 값이어야 한다.

람다(λ)는 L2 정규화 항이 얼마나 모델 학습에 영향을 미칠 것인지 조절한다. 람다는 매우 큰 가중치에 패널티를 주는 역할을 한다.
- 람다가 크면 L2 정규화 항(가중치 제곱의 합)이 작다는 말이므로 모델이 단순하다는 뜻이다. 따라서 이 모델 학습에는 데이터가 과소적합해질 우려가 있다.
- 람다가 작으면 L2 정규화 항(가중치 제곱의 합)이 크다는 말이므로 모델이 복잡하다는 뜻이다. 따라서 이 모델 학습에는 데이터가 과적합해질 우려가 있다.
적절한 람다의 값을 찾는 것은 모델 학습에 매우 중요한 일이다.
L1 정규화 : 고차원 특성 교차, 고차원 희소 벡터 사용 시
L2 정규화도 좋지만 모델 사이즈와 모델 학습 때 사용하는 메모리의 양을 줄이려면 어떻게 하는 게 좋을까?
우리가 희소 벡터/특성 교차를 이용해 모델을 만든다고 상상하자(희소 벡터란 원-핫 인코딩을 통해 만들어진 벡터, [0,0,0,0,0,1,0,0,0,0,0] 이런 식으로 표현, 특성 교차란 A x B, 두가지 특성의 곱).
첫번째 특성(x1)은 서치 쿼리로 인해 얻어지는 단어이고 두번째 특성(x2)은 동영상을 보고 얻어지는 무언가라고 한다면 첫번째 특성과 두번째 특성을 곱한 특성 교차인 x3(x1*x1)는 엄청나게 복잡할 것이다. 엄청나게 많은 동영상과 엄청나게 많은 단어들을 포함할 것이다(+ 엄청나게 많은 coefficient!).이렇게 된다면 이 특성교차를 이용해 머신러닝을 하는 것은 너무나 많은 메모리를 사용하게 된다. 런타임 오류가 생길 수도 있고 컴퓨팅 시간이 너무 오래 걸릴 수도 있다.
이때는 L1 정규화를 이용하는 것이 바람직하다. 메모리를 절약할 수 있고 또 데이터 과적합을 예방할 수도 있다.
그렇다면 구체적으로 L2 정규화와 L1 정규화의 차이가 무엇일까?
- L1 정규화는 필요없는 특성(feature)의 가중치 값을 0으로 떨어지게 해서 아예 연산 과정에서 없애버리고(이로 인해 컴퓨팅 시간, 사용하는 메모리 양 줄임) L2 정규화는 필요없는 특성의 가중치 값을 0에 가까워지게 하긴 하지만 정확히 0으로 바꾸진 않는다는 차이점이 있다.
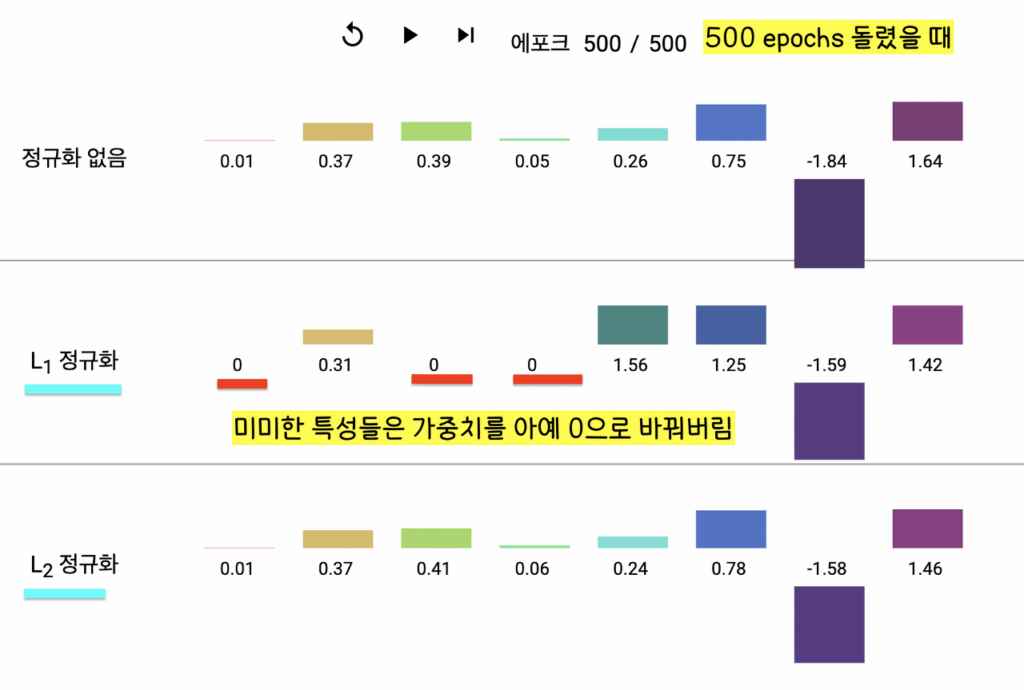
- 또한 수식으로 보면 정규화 항(Regularization term)에서 L1은 가중치의 절대 값을 더하고 L2는 가중치의 제곱을 더한다는 것을 볼 수 있다.
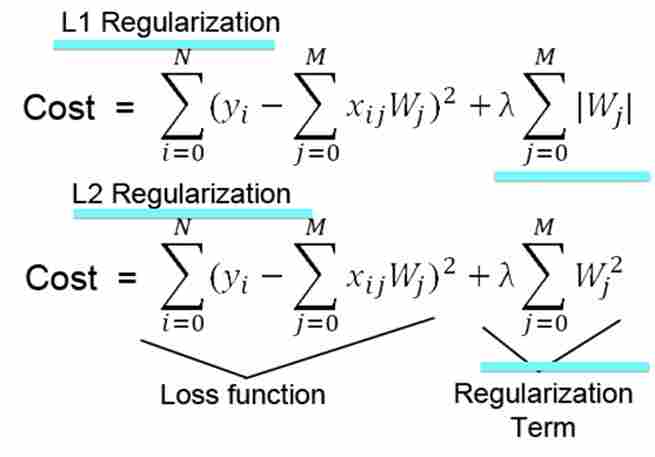
한줄 요약: 고차원 희소 벡터/특성 교차 머신 러닝 시 L1 정규화를 사용해서 안 쓰는 feature들 다 날려버리며 중요한 것만 집중해서 컴퓨터 학습시키자! (L2 정규화 안 쓰는 이유: L2는 feature을 날려버리지 못한다. 가중치 값을 0으로 강제하지 못한다.)
로지스틱 회귀: label이 확률일 때 사용
Label이 확률일 경우 y값이 항상 0과 1 사이에 있어야 한다(보통 확률 문제의 경우 0은 거짓이고 1은 참으로 그 사이 값, 예를 들면 0.2라면 0.2%의 확률로 참일 가능성이라는 뜻이다.)
y값이 0과 1 사이에 있기 위해서는 로지스틱 회귀 모델을 사용하는 것이 바람직하다. 로지스틱 회귀 모델은 시그모이드 함수를 사용해 만든다.
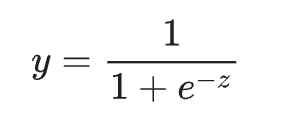

머신 러닝 모델을 로지스틱 회귀 모델로 만들면 아래의 그림과 같다.
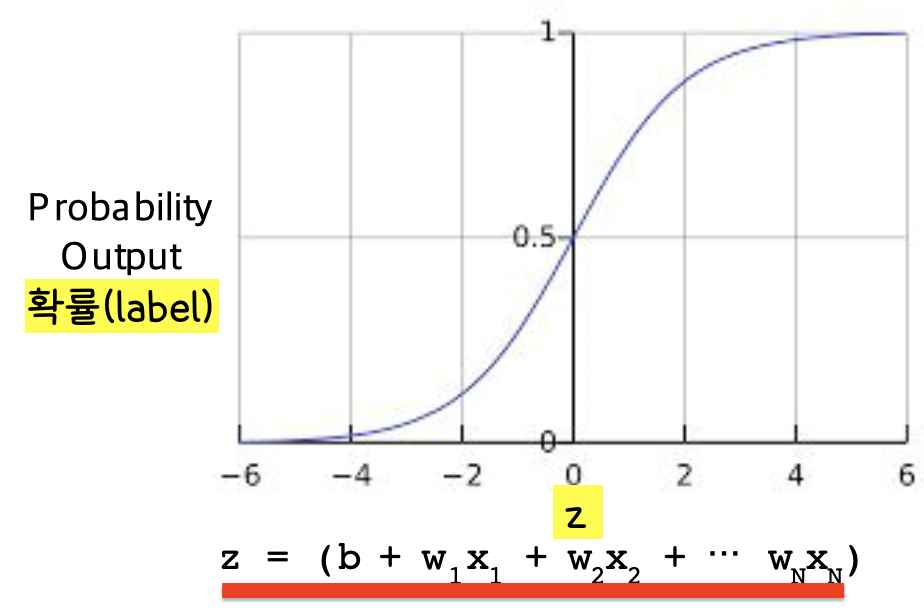
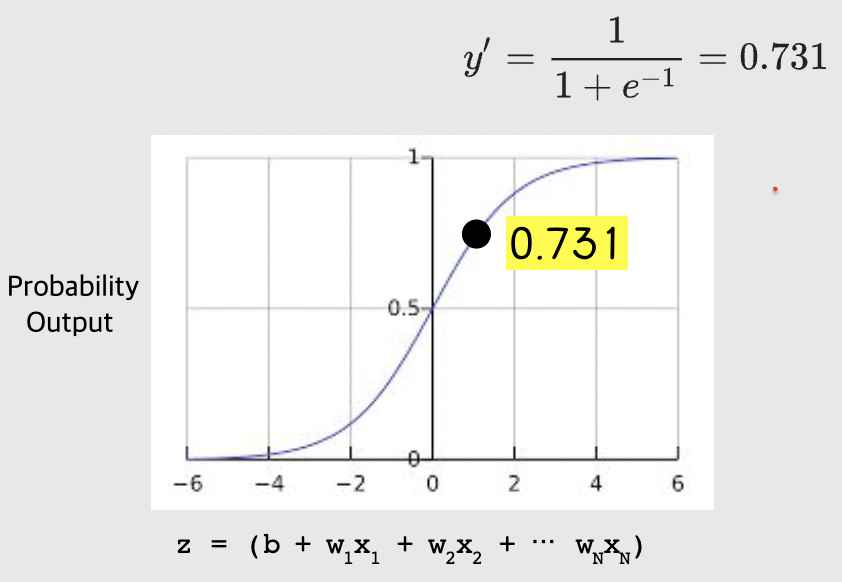
만약 우리의 모델이 b=1, w1=2, w2=-1, w3=5의 편향과 가중치와 x1=0, x2=10, x3=2의 특성 값을 가진다면 우리 모델의 확률 값(로지스틱 회귀 예측 값)은 0.731이다. 이게 어떻게 나오냐면, 먼저 아래의 수식을 보자!

z값은 1 + 2*0 + -1*10 + 5*2 = 1이다. 이 z값을 이 수식 안에 넣어주면 y'(로지스틱 회귀 모델의 출력 값, label 값, 확률 값)은 1/(1+e^(-1))이다. 이 값은 0.731이 된다.
그렇다면 이 모델, 로지스틱 회귀 모델의 Loss function(손실 함수)는 어떻게 될까?
Loss function을 알아야지 모델을 학습시키니 이게 본래의 Loss function에서 어떻게 달라졌는지 한번 알아보자! 원래의 선형 회귀의 손실함수는(Linear Regression Loss Function)은 (관찰 값-예측 값)^2로 나타냈다(제곱 값).

하지만 로지스틱 회귀 모델의 손실함수는(Logistic Regression Loss Function)은 로그 값으로 아래와 같이 나타낸다.

여기서 y(관찰 값)이 0일 경우 Log Loss는 Σ-log(1-y’)이 되고 y값이 1일 경우 Log Loss는 Σ-log(y’)가 된다. (관찰 값이 1이라는 것은 예를 들면 동전이 뒤집힐 때라는 것이고 관찰 값이 0이라는 것은 예를 들면 동전이 뒤집히지 않을 때라고 이해하면 되겠다. Boolean 값으로 참/거짓으로 이해하면 쉽다.)
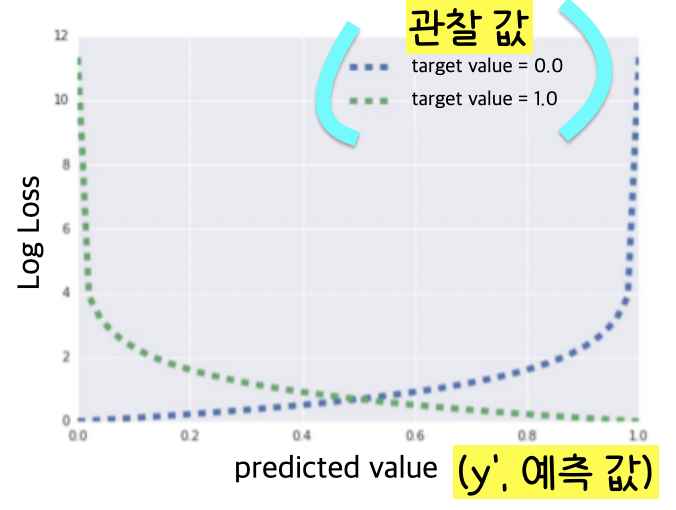
로지스틱 회귀 모델의 손실함수를 보면 y(관찰 값)가 1이고 y'(예측 값)이 0에 가까워질 때 Log Loss가 엄청나게 증가하는 것을 볼 수 있고 y(관찰 값)이 0이고 y'(예측 값)이 1에 가까워질 때 Log Loss가 엄청나게 증가하는 것을 볼 수 있다.
손실 함수가 급격하게 증가한다는 것은 모델 학습에 완.벽.히. 실패한다는 것을 의미하므로 손실을 줄이기 위해 정규화(Regularization, 위에서 계속 설명한 것)가 꼭 필요하다는 것을 확인할 수 있다.
3탄도 마저 쓸게요 +_+! 좀만 기다려주세요! ㅎㅎ