로지스틱 회귀, 분류 임계값 정하기
2탄에서 로지스틱 회귀를 알아봤는데 이어서 써보겠다. 로지스틱 회귀는 결과적으로 확률을 label로 내놓는다. 그리고 이 확률은 바이너리 값(참/거짓)으로 변환될 수 있다. 메일이 스팸일 확률이 0.00023이라면 그 광고가 스팸이라고 말할 수 있다.
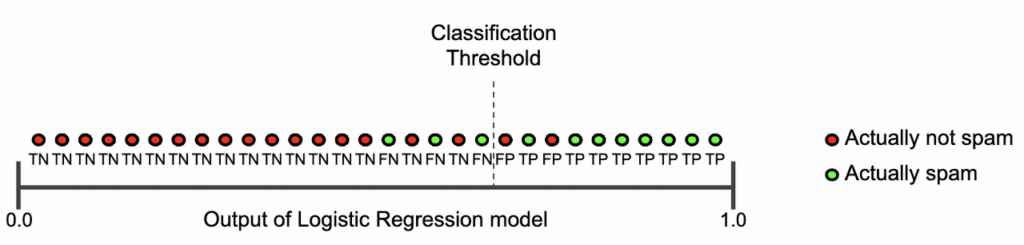
근데 만약 메일이 스팸일 확률이 0.6이라면 어떨까? 그 메일은 스팸일까 아닐까? 그냥 쉽게 쉽게 0.5 이상이면 참이고 0.5 미만이면 거짓이라고 말하면 모든 것이 쉽겠지만 실제로는 그렇게 적용할 수 없다. 따라서 우리는 분류 임계값을 정의해야한다.
분류 임계값 이상의 값을 가지는 이메일들은 스팸이고 분류 임계값 미만의 값을 가지는 이메일들은 스팸이 아니라고 분류한다.
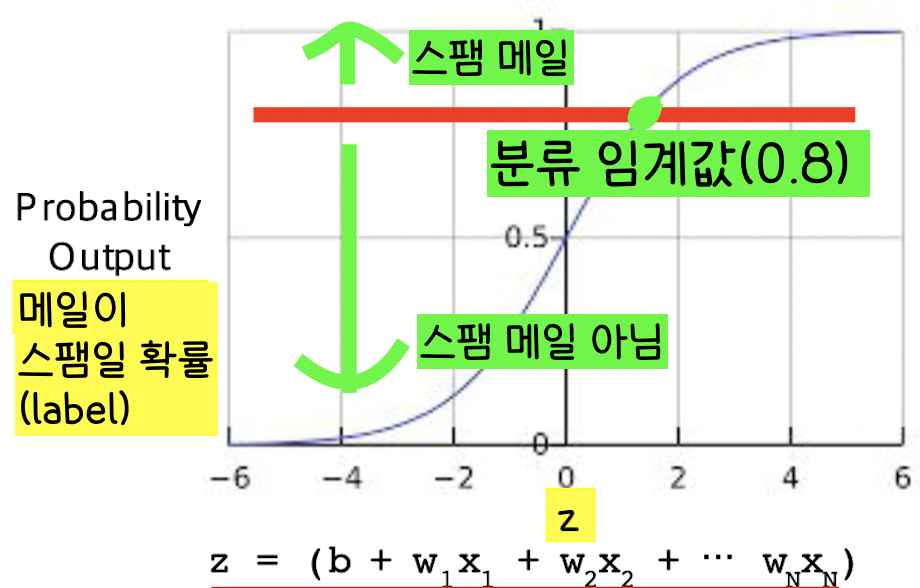
그렇다면 분류 임계값을 어떻게 정할까?
이상적인 분류 임계값을 정하기 위해선 우리가 현재 집중하고 있는 문제가 어떤 문제인지 정확히 이해하며 그 모델의 ROC 커브를 보고 정해야한다.
일단 우린 ROC 커브를 이해하는데 기초가 되는 True Positive, False Positive, False Negative, True Negative에 대해 알아보자.
True Positive(TP), False Positive(FP), False Negative(FN), True Negative(TN) 설명
우리가 잘 알고 있는 이솝 우화인 마을 사람들에게 ‘늑대다’라고 외치던/뻥치던 양치기 소년의 예시를 들면
- Positive는 양치기 소년이 늑대라고 말한 것
- Negative는 양치기 소년이 늑대라고 말하지 않은 것
- True는 양치기 소년의 말이 맞은 것(늑대라고 말했을 때 진짜 늑대이거나 or 늑대가 없다고 말했을 때 진짜 늑대가 없거나)
- False는 양치기 소년의 말이 틀린 것(늑대라고 말했을 때 늑대가 실제로 없거나 or 늑대가 없다고 말했을 때 진짜 늑대가 있거나)
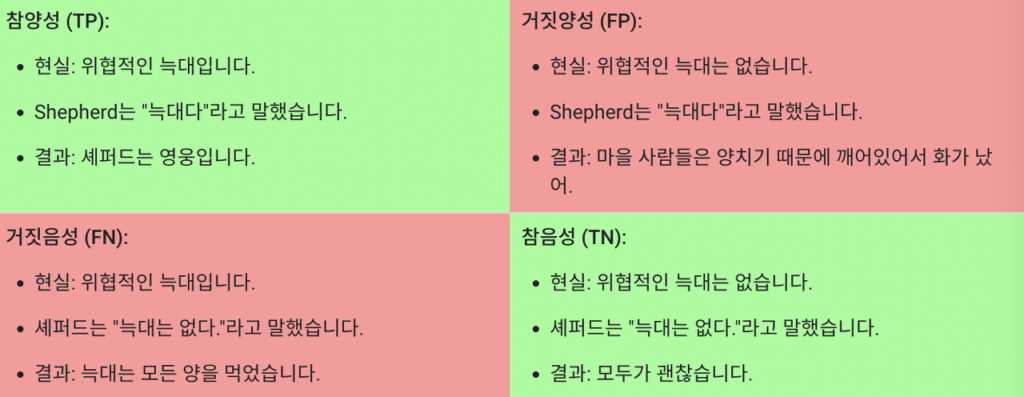
True positive는 positive한 결과를 제대로 예측한 결과이고
True negative는 negative한 결과를 제대로 예측한 결과이다.
False positive는 positive하지 않은 결과를 positive하다고 잘못 예측한 결과이고
False negative는 negative하지 않은 결과를 negative하다고 잘못 예측한 결과이다.
이제 TP, FP, FN, TN을 가지고 아래 데이터의 정확도를 측정해보자.
정확도(Accuracy)는 모델이 올바르게 예측한 확률을 나타낸다(= 모델이 올바르게 예측한 횟수 / 모델이 예측한 전체 횟수).

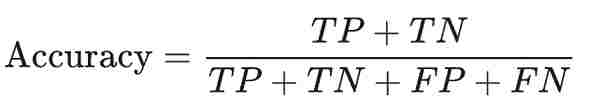
모델의 정확도는 (1+90)/(1+90+1+8) = 0.91이 된다. 100개의 예측 중 91개가 올바르다는 말이다. ‘음,, 모델의 정확도가 91%나 된다고? 꽤 정확한 머신러닝 모델 아니야?’라고 생각할 수 있지만 양성 종양의 케이스는 91개(TM 90개, FP 1개)이고 악성 종양의 케이스는 9개(TP 1개, FN 8개)이니 우리가 찾은 정확도가 악성 종양, 우리가 관심있게 보는 부분에 대한 정보를 제대로 전달하지 못한다고 말할 수 있다(데이터 부족).
*의사의 경우 양성 종양을 더 잘 알아보는 것보다 악성 종양을 더 잘 알아보는 것이 중요하다. 악성 종양은 사람의 목숨을 위협하기 때문! 이래서 우리가 해결하려는 문제의 성격을 잘 봐야 한다!
이와 같이 데이터 셋이 positive, negative 데이터 수가 극명하게 다를 경우 데이터의 accuracy를 찾는 것은 모델 학습에 별로 도움이 안된다. 이때는 정밀도와 재현율을 찾는 것이 도움이 된다.
이제 정밀도와 재현율에 대해 알아보자!
정밀도(Precision)는 모델이 positive하다고 예측한 횟수 중 진짜 positive했던 확률을 나타낸다(= 모델이 positive하다고 예측하고 진짜 positive한 횟수 / 모델이 positive하다고 예측한 전체 횟수)
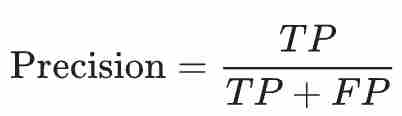
재현율(Recall)은 실제로 positive한 사례 중 모델이 positive라고 제대로 예측한 확률을 나타낸다(= 모델이 positive하다고 제대로 예측한 횟수 / 실제로 positive한 사례들)

모델이 얼마나 정확한지 평가하려면 정밀도와 재현율을 모두 봐야한다. 대부분의 경우, 정밀도와 재현율은 반비례 관계에 있다(정밀도가 높아지면 재현율은 낮아지고 정밀도가 낮아지면 재현율은 높아진다). 아래 예시를 한번 보자.

예시를 보면 Precision은 TP/(TP + FP) = 8/(8+2) = 0.8이고 Recall은 TP/(TP + FN) = 8/(8+3) = 0.73이다. 여기서 만약 분류 임계값을 높이면


Precision은 TP/(TP + FP) = 7/(7+1) = 0.88가 되고 Recall은 TP/(TP + FN) = 7/(7+4) = 0.64가 된다. 정밀도(Precision)는 높아지고 재현율(Recall)은 낮아졌다. 여기서 분류 임계값을 내리면


이번엔 Precision은 TP/(TP + FP) = 9/(9+3) = 0.75가 되고 Recall은 TP/(TP + FN) = 9/(9+2) = 0.82가 된다. 정밀도(Precision)는 낮아지고 재현율(Recall)은 높아졌다. 이렇게 정밀도와 재현율을 보면서 우리가 학습한 모델이 얼마나 정확한지 특정 분류 임계 값에 대해서 알아볼 수 있다.
하지만 가장 적절한 분류 임계값은 어떻게 구할까? 그건 바로 ROC 곡선을 보면 된다!!
ROC는 가능한 모든 분류 임계값에서 모델의 성능을 보여주는 그래프이다. 이 곡선은 x축에 거짓양성률(False Positive Rate, FPR), y축에 참양성률(True Positive Rate, TPR = 재현율)을 나타낸다.
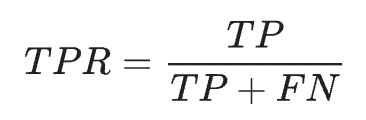
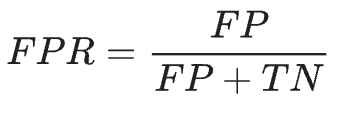
일반적인 ROC 곡선은 아래와 같다.
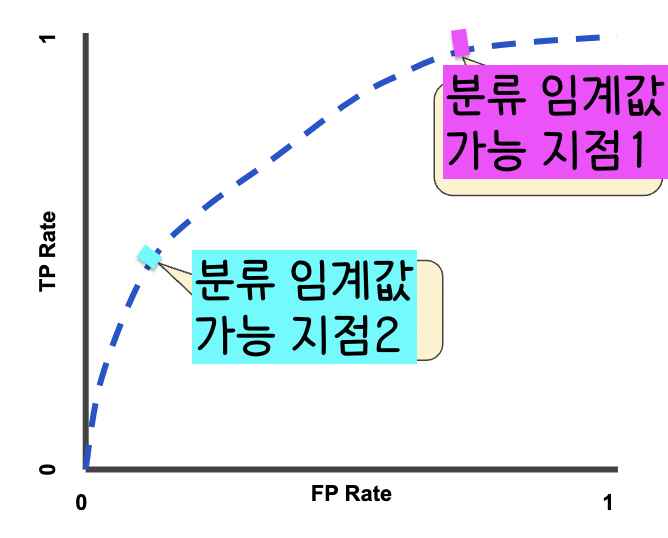
그래프 1을 보면 ROC 곡선에서 분류 임계값이 가능한 지점이 두 개가 있는 걸 볼 수 있다. 모델의 분류 임계값을 정하는데는 얼마나 많은 False Positive을 우리가 용인할 것인가 생각해보고 저 두 개의 지점 중 하나를 고르면 된다.(더 자세한 설명은 이 유튜브 영상에서 보세요~)
분류 임계값은 ROC로 구하는 걸 이제 알았고 이제는 ROC 곡선의 적분 값인 AUC에 대해 잠시 얘기해보겠다.
그래프 2를 보면 빨간 AUC, 파란 AUC를 볼 수 있다. 이 두 개의 AUC는 각기 다른 분류 방법을 사용한다. 만약 빨간 AUC가 로지스틱 회귀 방법을 사용하고 파란 AUC가 랜덤 포레스트 방법을 모델 분류 방법으로 사용한다면 우리는 빨간 AUC인 로지스틱 회귀 방법을 우리 모델에 사용하자고 말할 수 있다.
AUC 값이 클수록 그 분류 방법이 더 낫다고 말할 수 있다.
빨간색 AUC 분류 방법이 파란색 AUC 분류 방법보다 낫다.
신경망
비선형 분류 문제는 어떻게 풀어야 할까? 우리는 특성 교차를 이용해 비선형 분류 문제를 풀 수 있다고 이미 배웠다(특성 교차를 이용해 비선형 분류 문제를 푸는 방법은 여기). 하지만 모든 비선형 분류 문제가 특성 교차를 이용해 풀리진 않는다. 특성 교차를 이용해 푸는 비선형 분류 문제는 데이터가 이런 식으로 나와있을 때고
데이터가 위의 그림과 같지 않고 더 복잡하다면, 아래의 그림과 같다면 우리는 특성 교차 말고 다른 방법을 찾아봐야한다. 그 방법은 바로 신경망을 이용하는 것이다.
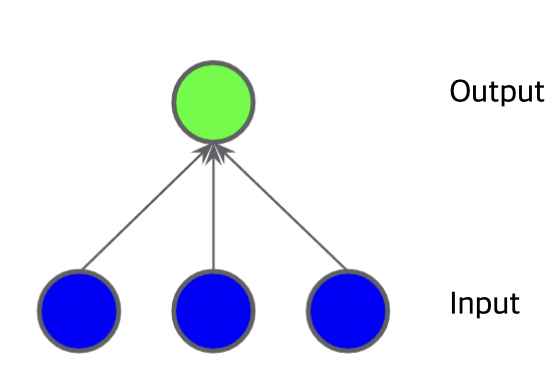
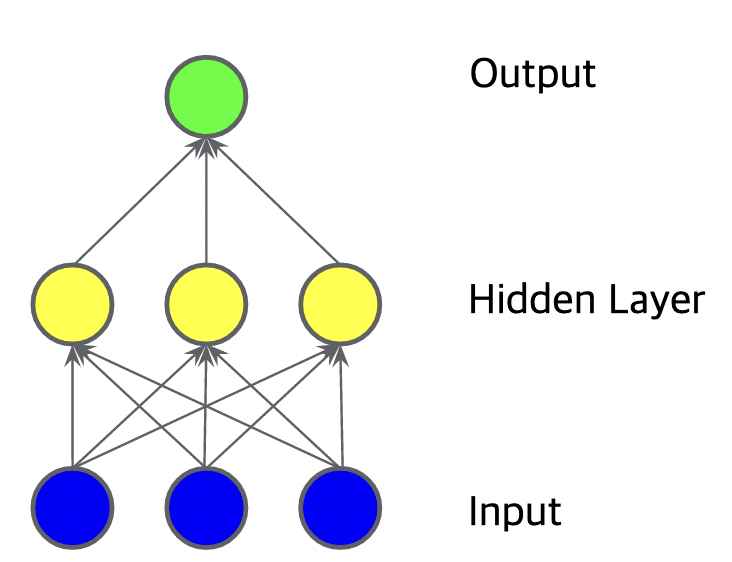
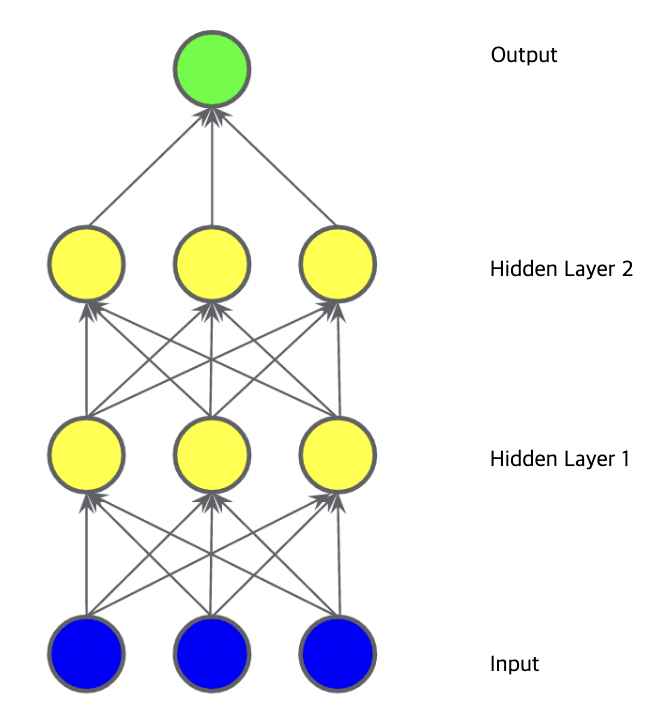
그림 1과 같은 데이터는 선형 모델로 해결할 수 없다. 그림 2,3,4와 같은 모델들은 모두 선형 모델이다. 히든 레이어도 output(아웃풋)=weight(가중치)*input(인풋)+bias(편향)의 방정식을 이용하므로 히든 레이어를 사용하는 그림 3,4도 모두 선형이다(선형 x 선형 = 선형).
비선형 문제를 풀기 위해서는 모델에 직접 비선형성을 도입해야 한다. 비선형성은 활성화 함수를 모델에 도입하면서 생긴다.

대표적인 활성화 함수는 시그모이드 함수, ReLU 함수가 있다.


시그모이드 함수는 output 값을 0과 1 사이의 값으로 변환시켜주는 함수이고 ReLU 함수는 0 이하의 값들을 모두 0으로 바꿔버리는 함수이다. 사실 다른 수학적 함수들도 활성화 함수의 역할을 할 수 있다. σ를 활성화 함수라고 친다면 노드들은 σ(w*x+b)로 나타낼 수 있다.
여기서 노드는 그림 5의 분홍색 동그라미를 말한다. 그림 5에는 3개의 노드가 있다. 각각의 노드는 σ(w*x+b)를 아웃풋으로 내보내고 그 다음 hidden layer 2에 우리가 받은 분홍색 동그라미의 아웃풋을 인풋으로 넣는다.
여기까지 우리는 신경망으로 비선형성 문제를 푸는 것을 알아봤다.
구글 머신러닝 crash course 정리 끝!